Adversarial Detection

Adversarial Detection: Attacking Object Detection in Real Time

Han Wu, Syed Yunas, Sareh Rowlands, Wenjie Ruan, and Johan Wahlstrom

Hi, everyone. I will present Adversarial Detection: Attacking Object Detection in Real Time. Some robotic applications rely on object detection models to perceive the environment.

For example, an autonomous driving system relies on object detection models to detect traffic signs and pedestrians.

Our research demonstrates that we can attack object detection models in real time. We can fabricate bounding boxes at desired locations. We can even specify which kind of traffic sign to fabricate. For example, the multi-untargeted attack generates all different kinds of traffic signs. We have 30, 60, the stop sign. While the multi-targeted attack only generates the desired traffic sign, we only have stop signs here.

Before introducing our method,

Adversarial Filter

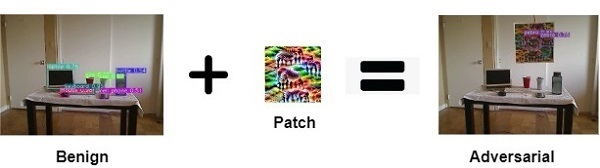
Adversarial Patch

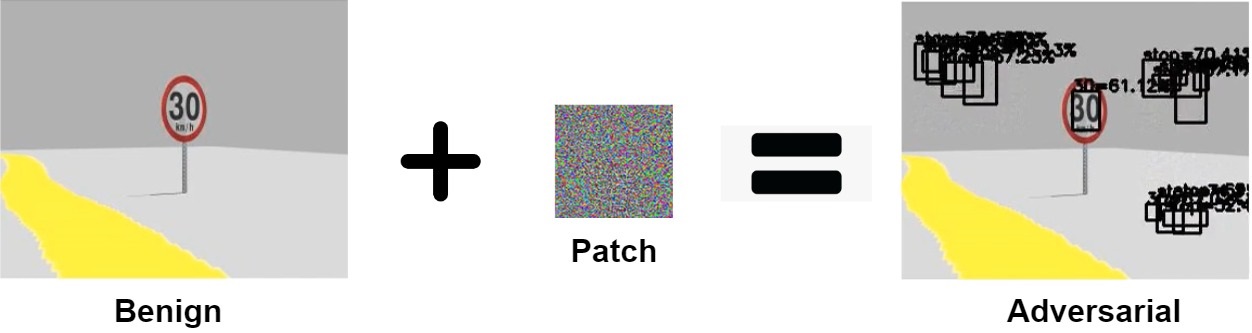
Adversarial Overlay

How different attacks apply the perturbation $\delta$ using a binary mask $m \in \{0, 1\}^{wh}$

$x^{'}_{filter} = x + \delta$ $x^{'}_{overlay} = x + m \odot \delta$ $x^{'}_{patch} = (1-m) \odot x + m \odot \delta$

Prior research used adversarial filter and adversarial patch to fool object detection models.

The Adversarial Filter applies the perturbation to the entire input image. The perturbation is unperceivable by human eyes. While the Adversarial Patch applies the perturbation to a small region of the input image, but the perturbation is perceivable by human eyes. Besides, the adversarial patch can control where we fabricate objects, while the adversarial filter cannot.

By combining adversarial filters' imperceptibility and adversarial patches' localizability, we generate adversarial overlays, which means we generate human unperceivable perturbation at a small region of the input image. Mathematically, we summarize how different methods apply the pertubation in different ways.

Given an input image $x$, the object detection model outputs $S \times S$ candidate bounding boxes $o \in \mathcal{O}$ at three different scales.

Each candidate box $o^i$ contains $(b_x^i, b_y^i, b_w^i, b_h^i, c^i, p_1^i, p_2^i, ..., p_K^i)$ for K classes, where $0 \leq i \leq |\mathcal{O}|$.

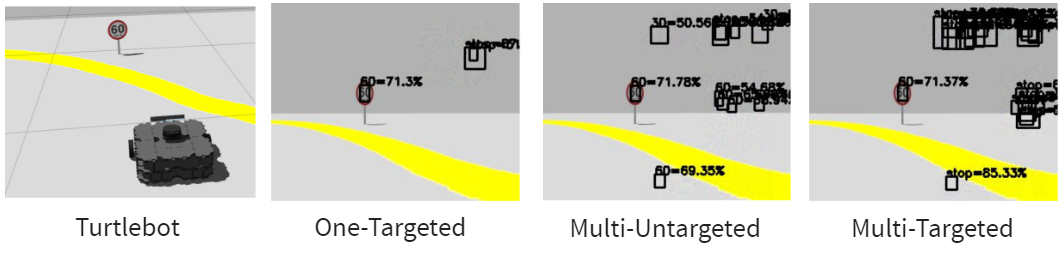
$$\begin{aligned} \text{One-Targeted}:\ \mathcal{L}_{adv}^{1}(\mathcal{O}) &= \max_{1 \leq i \leq |\mathcal{O}|}\ [\sigma(c^i) * \sigma(p^i_t)] \\ \text{Multi-Targeted}:\ \mathcal{L}_{adv}^{2}(\mathcal{O}) &= \sum^{|\mathcal{O}|}_{i = 1}\ [\sigma(c^i) * \sigma(p^i_t)] \\ \text{Multi-Untargeted}:\ \mathcal{L}_{adv}^{3}(\mathcal{O}) &= \sum^{|\mathcal{O}|}_{i = 1} \sum_{j=1}^{K}\ [\sigma(c^i) *\sigma(p^i_j)] \end{aligned}$$

where $|\mathcal{O}| = \sum_{1 \leq i \leq 3} S_i \times S_i \times B$, and $S_i$ represents the grid size of the $i_{th}$ output layer ($S \in \{13,26,52\}$, $B=3$).

Thanks

https://detection.wuhanstudio.uk

Source Code